Tree Data Structure Terminologies – Set 2
In our previous article on Tree Terminologies, we have seen basic tree terminologies like Nodes, Edges, Root, Parent, Children, Leaves and Siblings. In this article, we will understand Degree of Tree, Path, Level, Depth, Height and sub tree.
Degree
Total number of children of a node is called Degree of that node.
The Degree of a Tree is the maximum degree of node in a given tree. In our example tree, Degree of nodes A and D is 3. All the other nodes have less or equal degree. So the degree of our tree is 3.
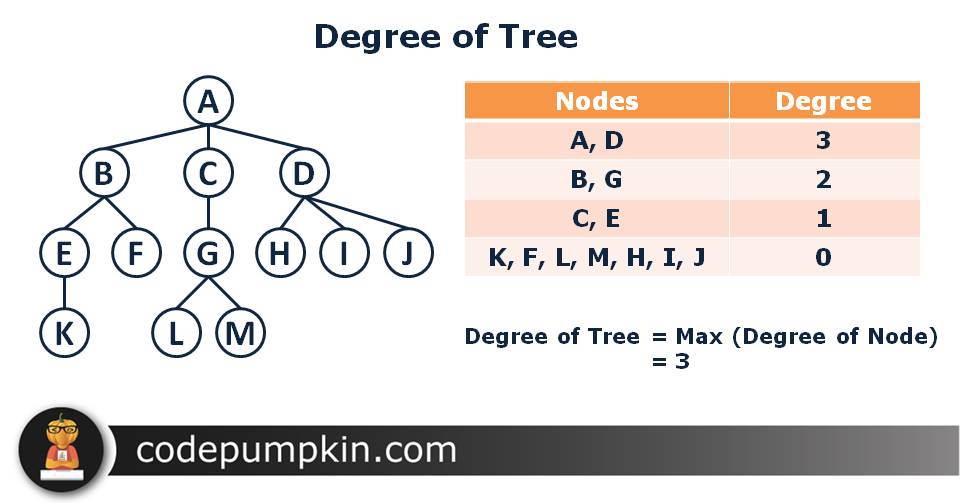
Terminal and Intermediate Nodes in terms of degree :
– A node with degree zero is called a terminal node or a leaf. In our example nodes K, F, L, M, H,I and J are leaf nodes.
– Any node whose degree is not zero is called non-terminal node. They are intermediate nodes in traversing the given tree from its root node to terminal nodes.
Path
A sequence of nodes and edges connecting a node with a descendant. A path starts from a node and ends at another descendant node or a leaf.

Notes :
– When we talk about path, it includes all the nodes and edges along the path and not just edges.
– The direction of path is strictly from top to bottom and it can not be changed at any point. For Example, In the diagram, we can't really talk about a path from D to K although D is above K. Also there will be no path starting from a leaf or from a child node to a parent node.
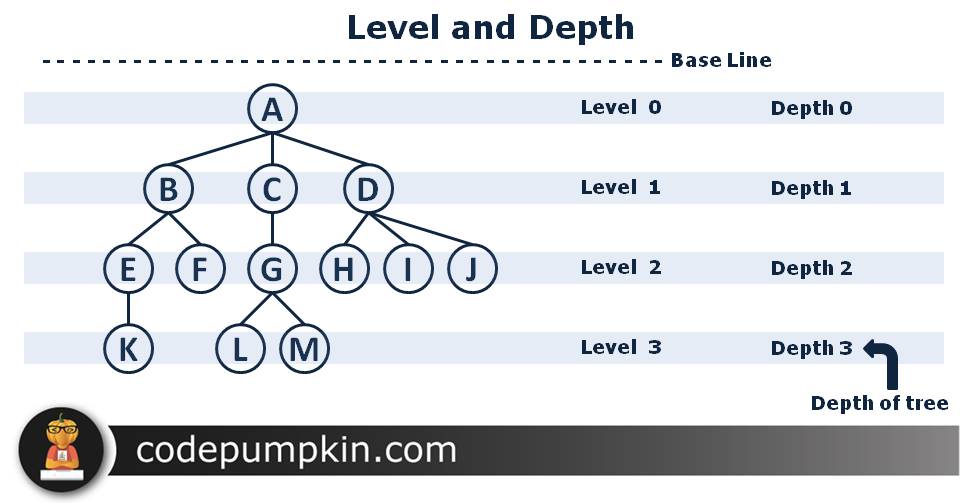
Level
The tree is structured in different levels. The entire tree is leveled in such a way that the root node is said to be at level 0, then its immediate children are at level 1 and their immediate children are at level 2 and so on up to the terminal nodes.
Base line for counting level is at the top of the tree and the Level count starts from 0 at root and increment by 1 at each Level. In other words, If a node is at level n, then its children will be at level n+1
Total number of edges from root node to particular node is called depth of that node. The total number of edges from root node to a leaf node in the longest path is said to be Depth of the tree.
In our example, depth of a root node A is zero and depth of a tree is 3. Base line of counting depth is also at the top of the tree like level.
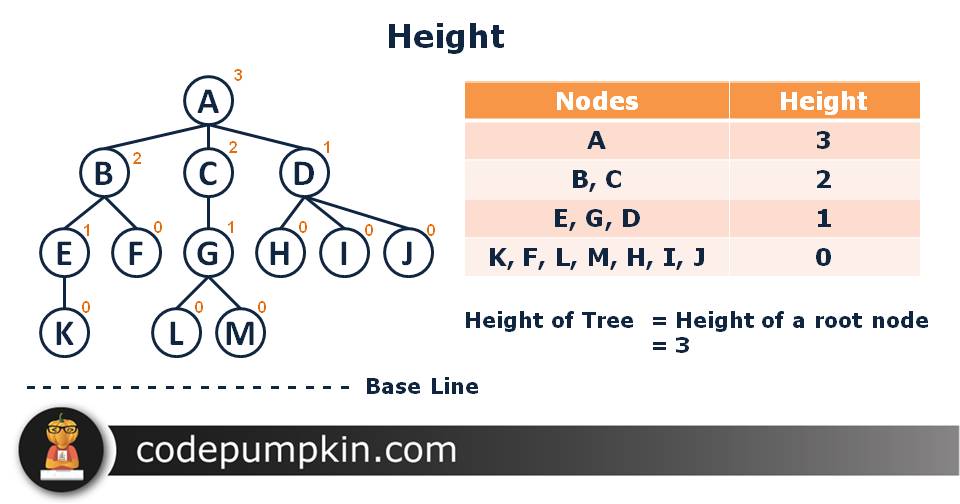
Height
The height of a node is the number of edges on the longest path from the node to a leaf. A leaf node will have a height of 0. Height of a root node is called Height of a tree.
Two nodes at the same level can have different height. For example, Height of G is 1, but height of H is 0 as it is leaf node.
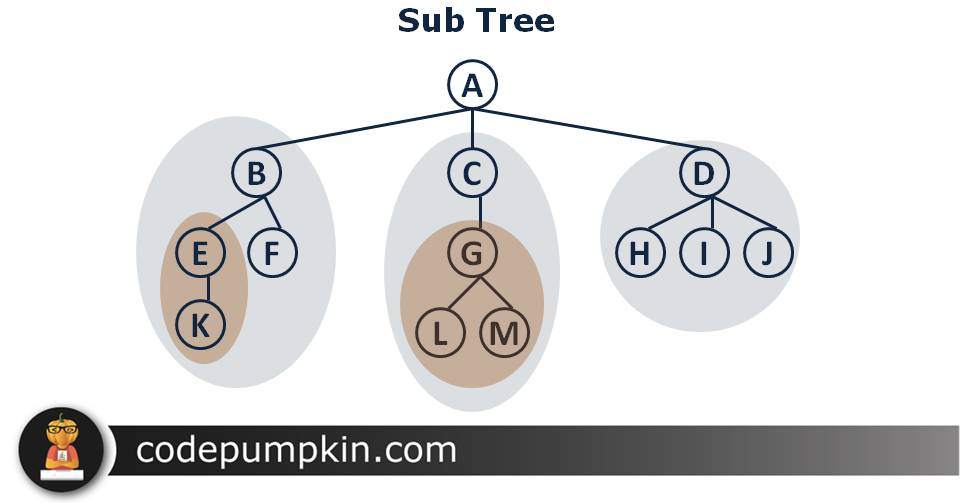
Sub Tree
In tree, each child from a node also forms a tree which is a subset of original tree and it is known as sub tree.
That's all for this topic. If you guys have any suggestions or queries, feel free to drop a comment. We would be happy to add that in our post. You can also contribute your articles by creating contributor account here.
Happy Learning 🙂
If you like the content on CodePumpkin and if you wish to do something for the community and the planet Earth, you can donate to our campaign for planting more trees at CodePumpkin Cauvery Calling Campaign.
We may not get time to plant a tree, but we can definitely donate ₹42 per Tree.
About the Author
Tags: DataStructure, Tree
Comments and Queries
If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example:<pre><code class="java"> String foo = "bar"; </code></pre>For more information on supported HTML tags in disqus comment, click here.