Trapping Rain Water | Algorithm Problem
In this article, we are going to solve the trapping water problem. This kind of problems are asked very frequently in interviews and online programming challenges.
Problem Statement
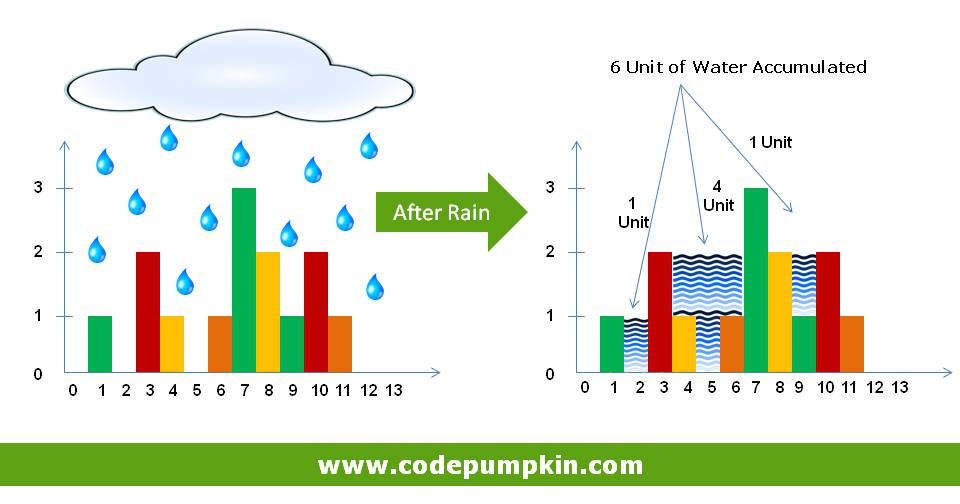
We need to find the maximum volume of water that can be stored in between buildings or bars as shown in the below image. Assume that width of each bar is 1.
In other words, Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
int arr[] = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};Answer : 6 Unit
Other Test Cases
Case 1 :
Input = [3, 0, 3]
Output = 3
Case 2 :
Input = [0, 4, 5, 1]
Output = 0
Case 3 :
Input = [ 1, 4, 2, 5, 0, 6, 2, 3, 4]
Output = 2 + 5 + 2 + 1
= 10
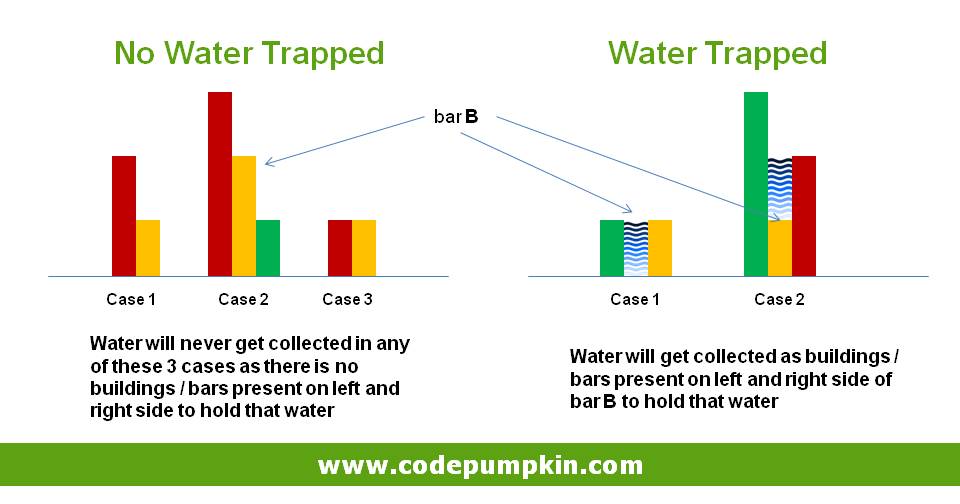
when will rain water be trapped on any Bar?
For water to get accumulated on bar B, there should be higher sized bars present on left and right side of that bar B. (i.e. bars with height greater than the hight of bar B)
How much rain water will be trapped on each bar?
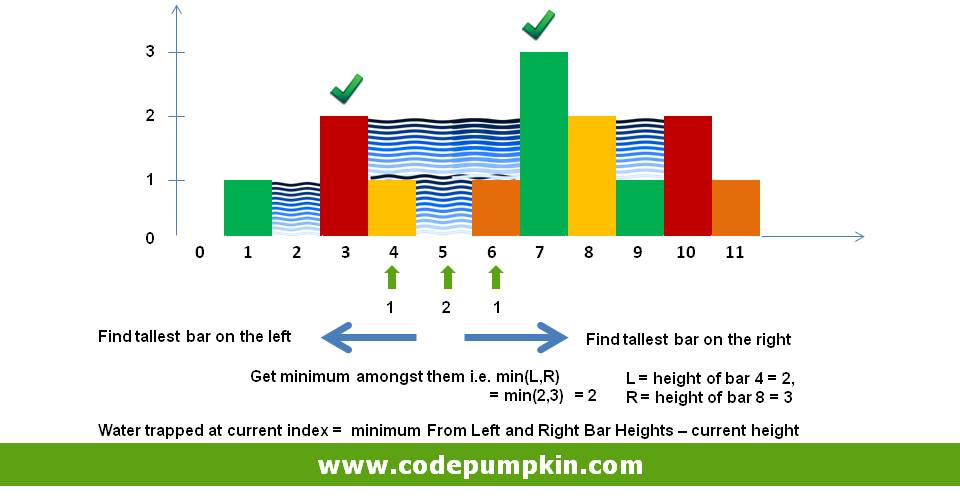
So for example,
water trapped at index 5 = min(2,3) – 1 = 1
index 6 = min(2,3) – 0 = 2
index 7 = min(2,3) – 1 = 1
Solution Approaches
Using above facts, we can think of two approaches to solve this problem:
Approach 1 (Naive Approach)
- Traverse every array element
-
For each element,
– Find the highest bars on left and right sides.
– Take the smaller of two heights.
– The difference between smaller height and height of current element is the amount of water that can be stored in this array element. -
Time complexity of this solution is O(n2) as
– we are traversing each element i.e. n times +
– for each element we are searching left and right bar with max hight i.e. again n times.
This is not very efficient solution for the given problem.
Approach 2
We can to prre-compute highest bar on left and right of every bar in O(n) time. Then use these pre-computed values to find the amount of water in every array element. This solution is O(n) and more efficient than the previous one.
We will implement the second solution:
Algorithm:
1. First compute highest bar on the left of every bar in O(n)
– by getting maximum between height of current bar and height of the previous tallest bar. Store this maximum value at the current index of left array.
2. Similarly compute highest bar on the right of every bar in O(n) and store it in right array.
Here is the graphical representation of above two steps.

3. Now at any point of the bar the maximum water that can be trapped will be minimum of left height and right height minus the height of the bar.
Amount of water stored on the top of the bar i = (maximum of left(i) and right(i)) – arr(i)
4. Keep adding the value for each bar.
Yeah… We solved it.
Below is the Java code for the same. This code input as below:
- First line of input contains a single integer N which is number of bars.
- Second line of input contains N non-negative integers ( A0 — A(n-1) ) which are height of each bar.
and it will print the output as number of unit we can hold between these bars.
package com.pumpkin.basic
import java.io.BufferedReader;
import java.io.InputStreamReader;
class TestClass {
public static void main(String args[]) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
String[] str = br.readLine().split(" ");
int[] arr = new int[n];
for(int i=0; i<n; i++)
{
arr[i] = Integer.parseInt(str[i]);
}
int[] left = new int[n];
int[] right = new int[n];
left[0] = arr[0];
for(int i=1; i<n; i++)
{
left[i] = Math.max(left[i-1],arr[i]);
}
right[n-1] = arr[n-1];
for(int i=n-2; i>=0; i--)
{
right[i] = Math.max(right[i+1],arr[i]);
}
int total = 0;
for(int i=0; i<n; i++)
{
total += Math.min(left[i],right[i]) - arr[i];
}
System.out.println(total);
}
}
You can also check the other articles on sorting and searching such as selection sort, binary search, fibonacci search, bubble sort etc. You will also like to enhance your knowledge by going through our other articles on different algorithms and data structures.
That's all for this topic. If you guys have any suggestions or queries, feel free to drop a comment. We would be happy to add that in our post. You can also contribute your articles by creating contributor account here.
Happy Learning 🙂
If you like the content on CodePumpkin and if you wish to do something for the community and the planet Earth, you can donate to our campaign for planting more trees at CodePumpkin Cauvery Calling Campaign.
We may not get time to plant a tree, but we can definitely donate ₹42 per Tree.
About the Authors
Tags: Algorithms, Array, Programming, RaeesLiquor, waterTrapping
Comments and Queries
If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example:<pre><code class="java"> String foo = "bar"; </code></pre>For more information on supported HTML tags in disqus comment, click here.