Program to find number of set bits in the Binary number
In this post, we will discuss about one of the easiest and commonly asked Bit Manipulation Interview Question i.e. Find total number of set bits in the given number?
There are many approach to solve this problem. Here, we will discuss about below two approaches:
1) & and >> Approach (naive Approach)
In this approach, we perform bitwise and (&) and bitwise right shift (>>) operations for each bit in a number.
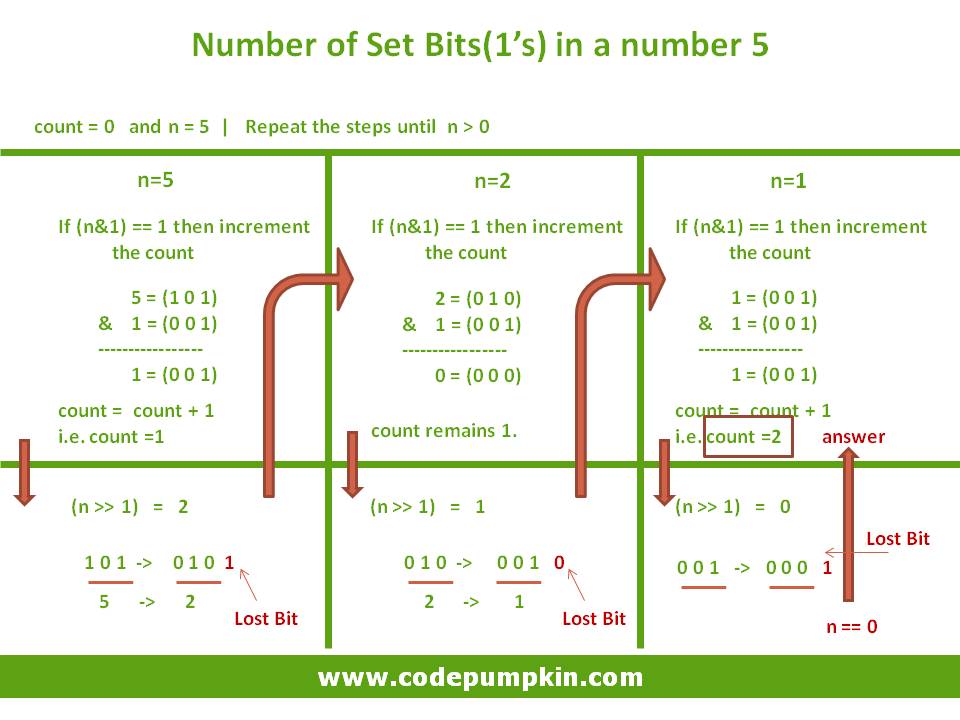
Step 1: (n&1) operation returns 1, if right most bit of the number is 1.
Step 2 : If this returns 1, we increment our counter.
Step 3 : perform n=(n>>1) , so that we can check the value of 2nd right most bit.
Continue this process, until n becomes 0.
Let's understand this by below example.
Java Program Implementation
public static int getNumberOfSetBitsApproachOne(int n){
int count = 0;
while(n>0)
{
if((n&1) == 1) // Similarly Condition (n&1)==0 can be used to calculate
{ //number of zeros in the given number
count++;
}
n = n>>1;
}
System.out.println(count);
return count;
}The naive approach requires one iteration per bit, until no more bits are set. So on a 32-bit word with only the high set, it will go through 32 iterations.
For Example, it will require 8 iiteraton to check number of set bits in number 128 (1000 0000)
2) Brian Kernighan's Approach
First of all, its not KerniGHAN, its pronounced as Kernihan, the G is silent 😉
This algorithm goes through as many iterations as there are set bits. So if we have a 32-bit word with only the high bit set, then it will only go once through the loop. For above Example of 128, it will give the answer only in one iteration.
In the worst case, it passes once per each bit and takes same time as naive approach. i.e. when all bits are 1 as in 255 (1111 1111)
What is Brian Kernighan's Approach?
It uses n = n & (n-1) approach.
If you perform bitwise & operation on n and (n-1), it produces the number with set bits one less than the original number. For example, if n has 4 set bits and if you perform n&(n-1), it produces the number with 3 set bits.
For example, let's try all the 4-bit combinations:
n n n-1 n&(n-1) -- ---- ---- ------- 0 0000 0111 0000 1 0001 0000 0000 2 0010 0001 0000 3 0011 0010 0010 4 0100 0011 0000 5 0101 0100 0100 6 0110 0101 0100 7 0111 0110 0110 8 1000 0111 0000 9 1001 1000 1000 10 1010 1001 1000 11 1011 1010 1010 12 1100 1011 1000 13 1101 1100 1100 14 1110 1101 1100 15 1111 1110 1110
So after performing each & operation, we will increment the counter. We will continue this process until n!=0
Java Program Implementation
public static int getNumberOfSetBitsApproach2(int n){
int count = 0;
while(n != 0){
n = n&(n-1);
count++;
}
System.out.println(count);
return count;
}We can use above two approaches to write a program to check if a given number is power of two or not?
That's all for this topic. If you guys have any suggestions or queries, feel free to drop a comment. We would be happy to add that in our post. You can also contribute your articles by creating contributor account here.
Happy Learning 🙂
If you like the content on CodePumpkin and if you wish to do something for the community and the planet Earth, you can donate to our campaign for planting more trees at CodePumpkin Cauvery Calling Campaign.
We may not get time to plant a tree, but we can definitely donate ₹42 per Tree.
About the Author
Tags: Bit Manipulation, Bitwise Operators, Core Java, Right Shift Operation
Comments and Queries
If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example:<pre><code class="java"> String foo = "bar"; </code></pre>For more information on supported HTML tags in disqus comment, click here.