Graph Search – Depth First Search
Depth First Search(DFS): In depth first search, we start from the root node then traverse the graph layerwise until we reach the leaf or dead end. In short, One starts at the root and explores as far as possible along each branch before backtracking. To avoid infinite looping we will mark the visited nodes as visited. The below image will illustrate the same.
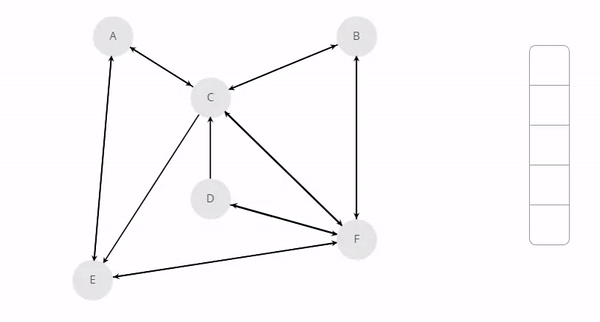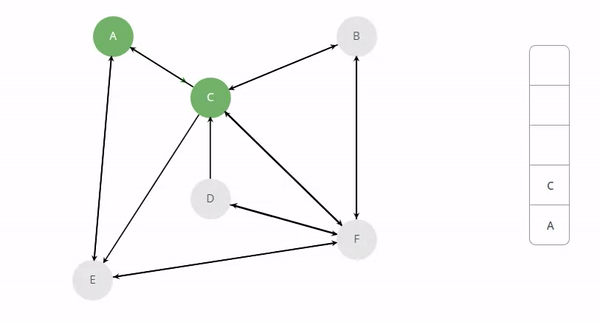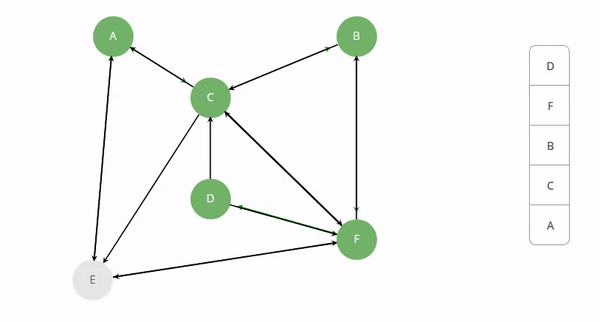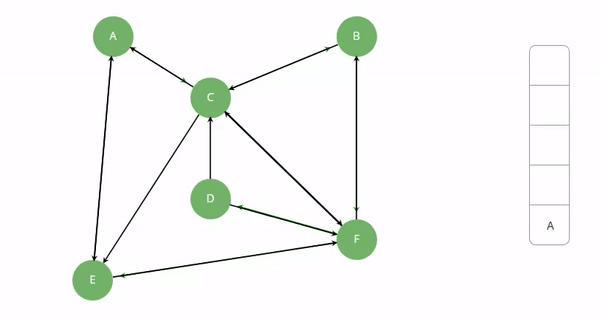
DFS Implementation:
As the name suggest in DFS, we will first visit the root node and push all its adjacent nodes into a stack. Pop a node from stack to select the next node to visit and push all its adjacent nodes into a stack. Repeat this process until the stack is empty. Here we have to make sure that we keep marking the visited nodes to avoid any cycle that exist in the Graph. So we will push node which are not visited. We will use recursion so we will be using method call stack as stack here.
The basic algorithm implementation will be as below:
function DFS(G,v):
label v as visited
for all edges from v to w in G.adjacentEdges(v) do
if vertex w is not labeled as visited then
recursively call DFS(G,w)
The implementation in java will be as below:
void dfsUtil(int v, boolean visited[]) {
visited[v] = true;
int n;
Iterator<Integer> itr = adj[v].iterator();
while (itr.hasNext()) {
n = itr.next();
if (!visited[n]) {
dfsUtil(n, visited);
}
}
}Download Complete Java Program »
We have used the adjacency list representation of graph here. The time complexity for the above implementation will be O(V+E), while in case of adjacency matrix representation it will be O(V2).
Applications:
- Testing whether graph is connected.
- Computing a spanning forest of graph.
- Computing, for every vertex in graph, a path with the minimum number of edges between start vertex and current vertex or reporting that no such path exists.
- Computing a cycle in graph or reporting that no such cycle exists.
I have also attached a graph class with DFS implementation which you can refer.
These algorithms are for searching elements in graph data structure, however we have also written articles on various search algorithms for array or list like Binary Search and Fibonacci Search.
You will also like to enhance your knowledge by going through our other articles on different algorithms and data structures.
That's all for this topic. If you guys have any suggestions or queries, feel free to drop a comment. We would be happy to add that in our post. You can also contribute your articles by creating contributor account here.
Happy Learning 🙂
If you like the content on CodePumpkin and if you wish to do something for the community and the planet Earth, you can donate to our campaign for planting more trees at CodePumpkin Cauvery Calling Campaign.
We may not get time to plant a tree, but we can definitely donate ₹42 per Tree.
About the Author
Tags: DataStructure, Depth First Search, Graph, Java, Stack Application
Comments and Queries
If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example:<pre><code class="java"> String foo = "bar"; </code></pre>For more information on supported HTML tags in disqus comment, click here.