Merge Sort is a Divide and Conquer algorithm. Divide and conquer algorithms divide the original data into smaller sets of data to solve the problem.

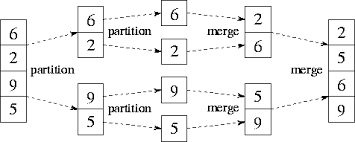
During the Mergesort process, the elements of the array or collections are divided into two parts. To split an array, Mergesort will take the middle element of the array and split the array into its left and its right part. The resulting sub arrays are again recursively divided into two sub parts until the size of the each subarray becomes 1.

Once the splitting process completes, merging process starts recursively which combines results of all the subarrays.

To combine both arrays, merging starts in each subarray at the beginning. It picks the smaller element and inserts this element into the beginning of the combined subarray. Then it compares the remaining elements of the two subarray and store them into combined sorted array. at the end of this, it produces combined sorted output array.

Algorithm

The logic for the merge sort is as follow:

• Divide : The first step would be to divide the problem into two or more than two sub-problems. As already stated, the input is an array containing N elements, this algorithm divides the array into two sub-arrays containing half of element in each of them, i.e. N/2. So division step is straight forward; just find the mid element in the array and divide it.
• The second step would be to solve these subproblems recursively until we reach to the base case where the solution is direct which is the subarray have only single elements which itself is sorted.
   
• Conquer : The third step would be to combine the solution of individual sub-problems to formulate the overall solution to our problem.

The above three steps are also illustrated in above GIF image as well as below diagram:

In short, the algorithm for merge sort will be divided into two main parts

1. Divide the input array into subarrays and after that
2. Merge all the arrays to form the sorted array.

Java Program Implementation

public class MergeSortExample {

	public static void main(String[] args) {
		int[] inputArr = {4,1,7,5,3,2,6};
		MergeSort ms = new MergeSort(inputArr);
		
		
		System.out.println("------------------\n Input \n------------------");
		ms.display();
		ms.sort();
		
		System.out.println("\n\n------------------\n After mergeSort() \n------------------");
		ms.display();
	}

}

class MergeSort{
	int[] arr;
	
	MergeSort(int[] arr)
	{
		this.arr = arr;
	}
	
	/**
	 * Main mergeSort() function which will internally calls
	 * overloaded recursive mergeSort(left,right) function
	 */
	public void sort()
	{
		sort(0,arr.length-1);
	}
	
	/**
	 * Overloaded Recursive mergeSort() function
	 * 
	 * @param left	left index of the input array
	 * @param right	right index of the input array
	 */
	public void sort(int left,int right)
	{
		int middle;  // middle index of the input array
		if(left<right)
		{
			middle = (left+right)/2;
			sort(left,middle);   // to divide the array -  left Half
			sort(middle+1,right); // Right Half
			
			merge(left,middle,right); // to merge sorted left and right halves
		}
	}
	
	/**
	 * merge function which will be internally called from sort() method.
	 * 
	 * @param left 		left index of the input array
	 * @param middle 	middle index of the input array
	 * @param right 	right index of the input array
	 */
	public void merge(int left,int middle,int right)
	{
		int n1,n2;
		int[] leftArray, rightArray;
		n1 = middle-left+1;
		n2 = right-middle;
		
		// Temporary left and right array
		leftArray = new int[n1];
		rightArray = new int[n2];
		
		for(int i=0; i<n1; i++)
		{
			leftArray[i]=arr[left+i];
		}
		for(int j=0;j<n2;j++)
		{
			rightArray[j]=arr[middle+1+j];
		}
		
		int i=0, 
			j=0, 
			k=left;
		
		while(i<leftArray.length && j<rightArray.length)
		{
			if(leftArray[i] &lt; = rightArray[j])
			{
				arr[k] = leftArray[i];
				i++;
			}
			else
			{
				arr[k] = rightArray[j];
				j++;
			}
			k++;
		}
		
		while(i<leftArray.length)
		{
			arr[k] = leftArray[i];
			k++;
			i++;
		}
		while(j<rightArray.length)
		{
			arr[k] = rightArray[j];
			k++;
			j++;
		}
		
	}
	
	
	/**
	 * Function to display Array
	 */
	public void display()
	{
		for(int i=0;i<arr.length;i++)
		{
			System.out.print(" " + arr[i]);
		}
	}
}

Time Complexity

From the algorithm we can see that it is a recursive algorithm and the time complexity for the same can be calculated as below: 

T(n) = 2T(n/2) +  which is resolved to O(n logn) time complexity.

Space Complexity

It is having O(n) space complexity.

Advantage

• It is more efficient as it is in worst case also the runtime is O(nlogn)
• It provides stable sorting.

Disadvantage

• It is takes lots of space(O(n)) which may slower down operations for the last data sets in some cases.

Java and many other languages use merge sort as default technique for sorting objects.

You can also check the other articles on sorting and searching such as selection sort, binary search, fibonacci search, bubble sort etc.  You will also like to enhance your knowledge by going through our other articles on different algorithms and data structures.